How did Turing apply the diagonal method? - Revisiting Turing's 1936 paper
Contents
I. Introduction
II. Turing’s criticism of the traditional diagonal method - Inappropriate presupposition
III. Turing’s proof - the essence of undecidability
IV. Conclusion
Appendix. Some basic concepts from Turing's 1936 paper
I. Introduction
Turing's 1936 paper is, as its title suggests, On Computable Numbers, with an Application to the Entscheidungsproblem [1].
The computable number is defined by Turing as the real in terms of its binary number representation computed by the computing machine (Turing Machine), and it is used to express the integrative concept of computability (see Appendix). Thus, the computable number becomes a guiding thread through Turing's 1936 paper.
The Entscheidungsproblem (decision problem) is derived from the 10th problem, Determination of the solvability of a diophantine equation, of the 23 mathematical problems formulated by Hilbert at the International Congress of Mathematicians in Paris in 1900 [2]. A general formulation of decision problem in the first-order predicate system is to ask [3]: is there a general process for determining whether a given first-order predicate formula is provable?
The focus of Turing's proof is in §8, Application of the diagonal process, which proves that there is no general process (computing machine) for determining whether a given computing machine can write down a computable number, i.e., the computability of computing machine is undecidable, thus revealing the essence of undecidability. In the final chapter §11, Application to the Entscheidungsproblem, Turing applies the results of §8 on computable numbers to prove that the Entscheidungsproblem is unsolvable, i.e., that there is no general process for determining whether any first-order predicate formula is provable.
It is worth noting that although Turing ostensibly applied Cantor's diagonal method [4], Turing did not copy Cantor's diagonal method, but rather took a critical inheritance attitude, first revealing an inappropriate presupposition hidden in Cantor's diagonal method, then revising it, and finally presenting a proof of the correct use of the diagonal method.
Unfortunately, the work of Turing's 1936 paper has been reduced to a cartoonish version of the halting problem, which has prevented a deeper understanding of the essence of undecidability!
II. Turing’s criticism of the traditional diagonal method - Inappropriate presupposition
- Turing's criticism
In §8, Application of the diagonal process, Turing first summarized the idea of applying the traditional diagonal method to prove that computable numbers (computable sequences) are unenumerable ([1] p. 246):
- Or we might apply the diagonal process. ‘‘If the computable sequences are enumerable, let an be the n-th computable sequence, and let Φn(m) be the m-th figure in an. Let β be the sequence with 1-Φn(n) as its n-th figure. Since β is computable, there exists a number K such that 1-Φn(n) = Φk(n) all n. Putting n=K , we have 1=2ΦK(K), i.e. 1 is even. This is impossible. The computable sequences are therefore not enumerable.
We schematize the enumeration process of the traditional diagonal method as follows:
a1 : Φ1(1) Φ1(2) Φ1(3) … Φ1(K) … // 100…0…
a2 : Φ2(1) Φ2(2) Φ2(3) … Φ2(K) … // 000…0…
a3 : Φ3(1) Φ3(2) Φ3(3) … Φ3(K) … // 010…1…
…
an : Φn(1) Φn(2) Φn(3) … Φn(K) … // 010…1…
…
aK : ΦK(1) ΦK(2) ΦK(3) … ΦK(K) … // 000…1…
…
where,
diagonal β’: Φ1(1), Φ2(2), Φ3(3), … Φn(K), … ΦK(K) …
inverted diagonal β : 1-Φ1(1), 1-Φ2(2), 1-Φ3(3), … 1-Φn(K), … 1-ΦK(K) …
The description number (D.N) of a computing machine is an encoding proposed by Turing (see Appendix), and computing machines are classed as circular and circle-free: a circle-free machine is a computing machine that writes down a computable number (computable sequence), while a circular machine is a computing machine that cannot write down a computable number. Therefore, the problem of determining whether a given number is a description number (D.N) of a circle-free machine means the problem of determining whether a given machine is computable.
Turing then criticized the above traditional diagonal method, revealing the inappropriate presuppositions hidden in it ([1] p. 246):
- The fallacy in this argument lies in the assumption that β is computable. It would be true if we could enumerate the computable sequences by finite means, but the problem of enumerating computable sequences is equivalent to the problem of finding out whether a given number is the D.N of a circle-free machine, and we have no general process for doing this in a finite number of steps. In fact, by applying the diagonal process argument correctly, we can show that there cannot be any such general process.
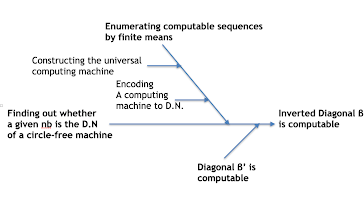
We schematize Turing's analysis in Figure 1.
That is, from a causal point of view, the conclusion that « β is computable » depends on several premises, one of which is that there exists a machine D finding out whether a given number is the D.N of a circle-free machine. However, this is an unasked question, and in fact Turing's following proof shows that such a machine doesn’t exist; in other words, it is an inappropriate presupposition to assume that such a machine exists .
2. The fallacy of inappropriate presuppositions [5]
An inappropriate presuppositions means that there are assumptions hidden in a question or reasoning that cannot be reasonably accepted in the relevant context.
The fallacy of inappropriate presuppositions stems from the failure to realize that the problem to be addressed has complex hierarchies and causality, and it is a trap of thought deeply hidden and difficult to detect which prevents the pursuit of more fundamental issues, thereby obscurities the essence of the problem.
A typical example of an inappropriate presupposition is a question such as, Have you stopped smoking?, which is a yes/no question, so there are only two answers:
- yes, I stop smoking.
- no, I still smoke.
But a yes or no answer is an admission that I used to smoke, however this is a question that is not asked, and its answer is implicated in the question, Have you stopped smoking?
Therefore, when dealing with such a complex issue, one should first reveal the underlying questions, rather than give a direct yes or no answer.
For example, let’s decompose the question Have you stopped smoking into two questions:
(1) Have you ever smoked?
(2) If so, have you stopped smoking?
Obviously, if the answer to question (1) is negative, i.e., I have never smoked, then question (2) would not become a question.
Turing's criticism of Cantor's diagonal method reveals precisely that there exists a general process for determining whether any machine is computable, which is in fact an inappropriate presupposition (Figure 1).
III. Turing’s proof - the essence of undecidability
Based on the above criticism, Turing proposed the correct application of the diagonal method prove that there is no general process for determining the computability of a machine, i.e., for determining whether any description number is a circle-free machine.
Turing said ([1] p. 246):
- The simplest and most direct proof of this is by showing that, if this general process exists, then there is a machine which computes β. This proof, although perfectly sound, has the disadvantage that it may leave the reader with a feeling that there must be something wrong. The proof which I shall give has not this disadvantage, and gives a certain insight into the significance of the idea circle-free. It depends not on constructing β, but on constructing β’, whose n-th figure is Φn(n).
Although Turing did not explain why computing β directly leaves the reader with a feeling that there must be something wrong, we can see from Figure 1 that β = (1-Φ1(1), 1-Φ2(2), 1-Φ3(3), ...) is inverted diagonal, while β' = (Φ1(1), Φ2(2), Φ3(3), ...) is diagonal, and that β depends on the existence of β', so Turing proposed to compute β' instead of β.
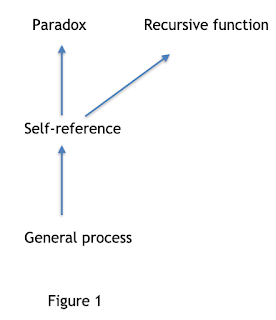
Turing used proof by contradiction to show that machine D does not exist: assuming that there exists a machine D to verify whether any machine writes down a computable number, Turing constructed a computable machine H that enumerates all computable numbers and computes the diagonal β' = (Φ1(1), Φ2(2), Φ3(3), ......) . However, the appearance of self-reference causes machine H to be unable to compute β' (circular), thus resulting in a contradiction that machine H is both computable (circle-free) and non-computable (circular). Therefore, Turing deduced that machine D does not exist.
Turing explained how to construct the machine H ([1], p. 247), which we illustrate in Figure 2:
- Let us suppose that there is such a process; that is to say, that we can invent a machine D which, when supplied with the S.D of any computing machine M will test this S.D and if M is circular will mark the S.D with the symbol u and if it is circle-free will mark it with s. By combining the machines D and U we could construct a machine H to compute the sequence β’.
- The machine H has its motion divided into sections. In the first N— 1 sections, among other things, the integers 1, 2,..., N— 1 have been written down and tested by the machine D. A certain number, say R(N— I), of section the machine D tests the number N. If N is satisfactory, i.e., if it is the D.N of a circle-free machine, then R(N)=1+R(N-1) and the first R(N) figures of the sequence of which a D.N is N are calculated. The R(N)-th figure of this sequence is written down as one of the figures of the sequence β’ computed by M. If N is not satisfactory, then R(N) = R(N— 1) and the machine goes on to the (N+1)-th section of its motion.
- From the construction of H we can see that H is circle-free. Each section of the motion of H comes to an end after a finite number of steps. For, by our assumption about D, the decision as to whether N is satisfactory is reached in a finite number of steps. If N is not satisfactory, then the N-th section is finished. If N is satisfactory, this means that the machine M(N) whose D.N is N is circle-free, and therefore its R(N)-th figure can be calculated in a finite number of steps. When this figure has been calculated and written down as the R(N)-th figure of β’, the iV-th section is finished. Hence H is circle-free.
- Now let K be the D.N of H. What does H do in the K-th section of its motion? It must test whether K is satisfactory, giving a verdict «s» or «u». Since K is the D.N of H and since H is circle-free, the verdict cannot be «u». On the other hand the verdict cannot be «s». For if it were, then in the K-th section of its motion H would be bound to compute the first R(K—1) + 1 = R(K) figures of the sequence computed by the machine with K as its D.N and to write down the R(K)-th as a figure of the sequence computed by H. The computation of the first R(K) — 1 figures would be carried out all right, but the instructions for calculating the R(K)-th would amount to « calculate the first R(K) figures computed by H and write down the R(K)-th ». This R(K)-th figure would never be found. I.e., H is circular, contrary both to what we have found in the last paragraph and to the verdict «s». Thus both verdicts are impossible and we conclude that there can be no machine D.
We also use an example from [6] to further illustrate how machine H works (Figure 3):
Machine H passes the numbers 1 through 13472 to machine D for testing and obtains 5 numbers that satisfy the requirements for circle-free machine coding, i.e., R(N) = 5, where β' = 10011.
Suppose H's own description number (D.N) is K = 4355 ... 3215 where the value of R(N) is 12, H eventually reaches the previous description number of its own description number, i.e., N = K-1 = 4335 ... 3214 which does not satisfy («u»), then H increments N to K = 4355 ... 3215, i.e., reaches its own description number: H passes it to machine D, and machine D must return satisfy («s»), then H must continue to run as defined because it is circle-free. Thus, H now increases R(N) from 12 to 13 and uses U to simulate it, but this means that H will simulate its own motion.
This simulation will initialize again R to 0 and run machine H until it reaches the 12-th figure, but it never reaches the 13-th figure. It then follows that H is circular rather than circle-free, contradicting the assumption that H is circle-free. Therefore, it follows that there is no machine D (Figure 1).
In other words, the traditional diagonal method hides an inappropriate presupposition: there exists a general process (machine D) that determines the computability of any computing machine, but in fact such a general process does not exist at the machine level.
IV. Conclusion
Turing, on the one hand, from the perspective of causality and hierarchy, had an insight into the inappropriate presupposition hidden in the traditional diagonal method, that is, the presupposition that there exists a general process that determines the computability of any machine; on the other hand, Turing realized that Cantor's diagonal method has the unique value of establishing an image for the concept of the abstract infinity.
So Turing neither discarded nor reproduced Cantor's diagonal method, but inherited it with a critical attitude, and was able to reveal the essence of undecidability, i.e., the computability of Turing Machine is undecidable.
We believe that revisiting of Turing's 1936 paper would be of substantial help in clearing up some of the fundamental puzzles that have plagued academia!
Appendix: Some concepts from Turing's 1936 paper
Computing machines ([1] p.232)
If an a-machine prints two kinds of symbols, of which the first kind (called figures) consists entirely of 0 and 1 (the others being called symbols of the second kind), then the machine will be called a computing machine. If the machine is supplied with a blank tape and set in motion, starting from the correct initial m-configuration, the subsequence of the symbols printed by it which are of the first kind will be called the sequence computed by the machine. The real number whose expression as a binary decimal is obtained by prefacing this sequence by a decimal point is called the number computed by the machine.
Circular and circle-free machines ([1] p.233)
If a computing machine never writes down more than a finite number of symbols of the first kind, it will be called circular. Otherwise it is said to be circle-free.
A machine will be circular if it reaches a configuration from which there is no possible move, or if it goes on moving, and possibly printing symbols of the second kind, but cannot print any more symbols of the first kind. The significance of the term "circular" will be explained in §8.
Computable sequences and numbers ([1] p.233)
A sequence is said to be computable if it can be computed by a circle-free machine. A number is computable if it differs by an integer from the number computed by a circle-free machine.
We shall avoid confusion by speaking more often of computable sequences than of computable numbers.
Example: a computing machine to compute the sequence 010101... ([1] p.233, p.240)
This is the first example of computing machine given by Turing in his paper that calculates the binary representation 010101… of the real 0.333… The table of rules is as follows:
q1 S0 PS1 R q2
q2 S0 PS0 R q3
q3 S0 PS2 R q4
q4 S0 PS0 R q1
Where, S0="#", S1="0", S2="1".
Simulate the run of this machine with the blank symbol # as input to the paper tape:
# # # # # # …
q1 q2 q3 q4 q1 q2 …
0 # 1 # 0 # …
Encoding of computable machines ([1] p.239)
To enumerate computable sequences, Turing encoded the computing machine:
Let us write down all expressions so formed from the table for the machine and separate them by semi-colons. In this way we obtain a complete description of the machine.
In this description we shall replace q{ by the letter "D" followed by the letter "A" repeated i times, and $,- by "D" followed by "C" repeated j times. This new description of the machine may be called the standard description (S.D). It is made up entirely from the letters "A", " C", "D", "L", "R", "N", and from « ;".
If finally wereplace "A" by "1", "C" by "2", "D" by "3"," L" by"4","R" by '5","N" by »6",and ";" by « 7 », we shall have a description of the machine in the form of an arabic numeral.
The integer represented by this numeral may be called a description number (D.N) of the machine. The D.N determine the S.D and the structure of the machine uniquely. The machine whose D.N is n may be described as M(n).
Our first standard form (the above example) would be :
q1S0PS1Rq2;q2S0PS0Rq3;q3S0PS2Rq4;q4S0PS0Rq1。
The standard description is :
DADDCRDAA;DAADDEDAAA;DAAADDCCRDAAAA;DAAADDRDA;
A description number is :
31332531173113353111731113322531111731111335317
A number which is a description number of a circle-free machine will be called a satisfactory number. In § 8 it is shown that there can be no general process for determining whether a given number is satisfactory or not.
Reference :
[1] https://www.cs.virginia.edu/~robins/Turing_Paper_1936.pdf
[2] David Hilbert: Mathematical Problems, http://aleph0.clarku.edu/~djoyce/hilbert/problems.html
[3] Hilbert and Ackermann, Grundziige der Theoretischen Logik (Principles of Theoretical Logic, Berlin, 1931), chapter 3.
[4] Georg Cantor, about the diagonal argument (translation in English), Deutsche Mathematiker-Vereinigung (Bd. I, S. 75-78 (1890-1)).
[5] Recognizing Fallacies/Fallacies of Presumption.
https://en.wikiversity.org/wiki/Recognizing_Fallacies/Fallacies_of_Presumption
[6] https://en.wikipedia.org/wiki/Turing%27s_proof



Commentaires
Enregistrer un commentaire