Liar's Paradox - Turing's Perspective vs. Gödel's Perspective

I. Introduction

The proof of Gödel's incompleteness theorem is found mainly in Chapter I and Chapter II of his 1931 paper [1]: in Chapter I, Gödel introduces the main idea of his proof, which is to construct a paradoxical proposition saying that it is itself unprovable by using the traditional Cantor’s diagonal method; in Chapter II, Gödel translates directly this paradoxical proposition in the formal system he defines, and claims that this paradoxical proposition is a « factual »  « undecidable proposition » in his formal system, thus concludes that his formal system is incomplete.

Gödel's paradoxical proposition is a replica of Liar's Paradox, so deciphering Liar's Paradox becomes a key point in deciphering the proof of Gödel's Incompleteness theorem!

II. Liar's paradox, self-reference and general processes

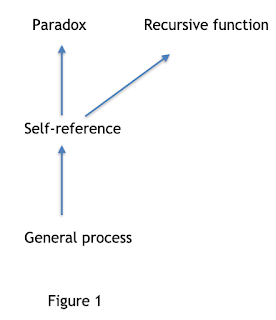
Liar's Paradox represents a class of paradoxes that are closely related to self-reference, and it can be said that self-reference is the « cause » of such paradoxes. However, self-reference is only a necessary condition for theses paradoxes, because self-reference does not necessarily produce a paradox, for example, self-reference of recursive functions is not a paradox.

Further, what is the «  cause »  of self-reference? It can be said that it is a general process f(x). A general process f(x) means that the variable x of f is any process, including f. Therefore, if x = f, then the self-reference is produced: f(f) (Figure 1). 


For Liar's Paradox, Epimenides says that all Cretans lie, denoted as Epimenides(cretan), where cretan is a variable. Since Epimenides is also a Cretan, making cretan=Epimenides produces the self-reference: Epimenides (Epimenides), where is the question: does Epimenides himself lie?

Thus, tracing the roots of paradoxes such as Liar's Paradox to general processes is just the subject of Turing's 1936 paper [2].

III. The main work of Turing’s 1936 paper

Turing's 1936 paper is centered around general processes: Turing starts with computable numbers, designs the Turing Machine (Computing Machine), defines the computability, encodes a Turing machine, and then designs a general process U(M) - the Universal Turing Machine - that simulates the computation of any Turing machine M.

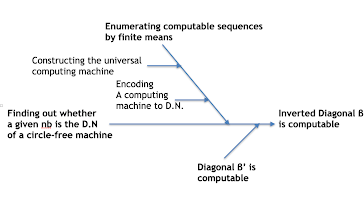
Turing then holds a critical attitude, first revealing the «  inappropriate presupposition »  of the traditional Cantor’s diagonal method, then revising it, and finally proposing the correct use of the diagonal method to prove that there exists no general process D(M) for determining the computability of any Turing machine M [3]. Thus Turing distinguishes the essential difference between a general process for computation U(M) and a general process for decision D(M): while U(M) is a Turing machine, D(M) is not (Figure 2). (In his 1938 doctoral dissertation, Turing proposes the concept «  Oracle »  to refer to D(M) [4]).


Turing continues to deduce that there exists no general process E(M) that determines whether any machine M prints the expected symbol (say 0).

Finally, Turing expresses a Turing machine M as a first-order predicate formula Un(M), and deduces that there exists no general process for determining whether any first-order predicate formula is provable, and so the Hilbert’s Entscheidungsproblem has no solution (Figure 3).

Contrary to the prevailing academic view of Turing's 1936 paper, Turing does not use paradoxes in his proof!

VI. Turing's and Gödel's different perspectives on the Liar's Paradox

Let us express Liar Paradox this way:

If Epimenides says that all Cretans lie (premise), does Epimenides himself lie (consequence)?

Gödel presupposes that Epimenides saying that all Cretans lie exists, and asks whether Epimenides himself lies; while Turing explores whether Epimenides saying that all Cretans lie exists. In other words, Gödel emphasizes effect, while Turing emphasizes cause.

It is necessary to mention here the last paper Turing left during his lifetime, "Solvable and Unsolvable Problems" (1954) [5]. Turing writes this paper in the form of popular science. Turing gives the example of a puzzle and uses proof by contradiction, supposing but not presupposing that there is a general process to determine whether any puzzle is solvable, and comes to a self-contradictory paradox. Then he concluded that there is no general process to determine whether any puzzle is solvable, so determining whether any puzzle is solvable is an undecidable problem.

Whether it is the 1936 paper or the 1954 paper, Turing is consistent in his view that paradoxes arise due to the presupposition of a general process for decision that do not otherwise exist.

V. Conclusion

Let us continue with Liar’s Paradox analogy.

Turing solved Hilbert's Entscheidungsproblem in 1936, the symbolic significance of which can be seen as revealing that Epimenides saying that all Cretans lied is not on Crete, but outside of it (Escher's style [6], Figure 4). This enables Turing to propose the «  imitation game  in 1950 that goes beyond the machine for computing to the machine for thinking and opens the chapter of artificial intelligence through machine learning [7]! 


Gödel, however, did not have such a systemic view without realizing that Epimenides saying that all Cretans lied is not inside Crete, but rather presupposed that Epimenides is inside Crete, thus Godel confused the two different dimensions of inside and outside Crete, producing Liar's Paradox (Escher's style [6], Figure 5). 


On the surface, Gödel's incompleteness theorem seems to give a profound conclusion about the incompleteness of formal systems, but in fact Gödel denies it, because in his proofs Gödel treats his self-contradictory paradoxical propositions as factual proposition of formal system, which causes unspeakable confusion in the mind of people for nearly a century.

Logically, Liar's paradox is a deeply hidden fallacy of "inappropriate presupposition"; cognitively, it forms a self-contradictory thought trap. Therefore, exploring the root of Liar's paradox and liberating the mind may be the real meaning of the meaningless Liar's paradox!

Reference

[1] Kurt Gödel, On Formally Undecidable Propositions of Principia Mathematica and Related Systems I (1931). https://monoskop.org/images/9/93/Kurt_G%C3%B6del_On_Formally_Undecidable_Propositions_of_Principia_Mathematica_and_Related_Systems_1992.pdf

[2] Alan Turing, On Computable Numbers, with an Application to the ENTSCHEIDUNGSPROBLEM, 1936. https://www.cs.virginia.edu/~robins/Turing_Paper_1936.pdf

[3] Yu LI, How did Turing apply the diagonal method? - Revisiting Turing's 1936 paper. https://revisiter-godel-article.blogspot.com/2023/11/revisiting-turings-1936-paper-how-did.html

[4] Turing, A.M. Systems of Logic Based on Ordinals, 1938.

[5] Alan Turing, Solvable and Unsolvable Problems. http://www.ivanociardelli.altervista.org/wp-content/uploads/2018/04/Solvable-and-unsolvable-problems.pdf

[6] https://mcescher.com/gallery/

[7] Alan Turing, Computing Machinery and Intelligence, 1950. https://academic.oup.com/mind/article/LIX/236/433/986238


Commentaires

Enregistrer un commentaire

Posts les plus consultés de ce blog

How did Turing apply the diagonal method? - Revisiting Turing's 1936 paper

Image
Contents I. Introduction II. Turing’s criticism of the traditional diagonal method - Inappropriate presupposition III. Turing’s proof - the essence of undecidability IV. Conclusion Appendix. Some basic concepts from Turing's 1936 paper I. Introduction Turing's 1936 paper is, as its title suggests, On Computable Numbers, with an Application to the Entscheidungsproblem [1]. The computable number is defined by Turing as the real in terms of its binary number representation computed by the computing machine (Turing Machine ), and it is used to express the integrative concept of computability (see Appendix). Thus, the computable number becomes a guiding thread through Turing's 1936 paper. The Entscheidungsproblem ( decision problem ) is derived from the 10th problem, Determination of the solvability of a diophantine equation , of the 23 mathematical problems formulated by Hilbert at the International Congress of Mathematicians in Paris in 1900 [2]. A general form
Lire la suite

Review of «  Complexity Theory’s 50-Year Journey to the Limits of Knowledge »

Image
The article «  Complexity Theory’s 50-Year Journey to the Limits of Knowledge »  [1] provides a fascinating review of the study of the P versus NP problem, especially tracing it back to Hilbert’s Project, where the Entscheidungsproblem appeared, and relating the P versus NP problem to the work of Gödel, Turing, and others, which gives the article an openness that is hard to see in similar articles!  The article is developed by the research career of Marco Carmosino, now a theoretical computer scientist at IBM: moving from an interest in Gödel's work to the study of the P versus NP problem. Faced with years of stagnation in the study of the P verses NP problem, Carmosino says, " It's one of the most obvious facts in theoretical computer science that when you come across a phenomenon that is so persistent, you need some explanation. " In an effort to break out of the P verses NP problem dilemma, Carmosino and some scholars have turned to the "Minimum Circuit Size
Lire la suite